¿ES
PUNTERO EL SECTOR AGRÍCOLA EN ALGUNA TÉCNICA O TECNOLOGÍA?
 |
| Escáner terrestre del GI AgróTICa y AP de la U. Lleida |
Evidentemente. Por ejemplo, se pondría a la
agricultura puntera en el uso de tecnologías genéticas, o en técnicas en biología, también en maquinaria. A pesar de ello, no es menos cierto que existen otros campos tecnologícos en los cuales los
agricultores “hemos ido a remolque”, y aquí se pueden citar como ejemplo aquellas
tecnologías en las que se combinan la electrónica y la computación.
Son conclusiones bastante lógicas cuando se
observan desde el prisma del interés económico/estratégico que hay en otros
sectores, y también, no se olvide, que la actividad agraria tiene el hándicap que
se “desenvuelve” en ambientes más “agresivos” y eso enmascara el uso de tecnología
“fina” porque es más fácil desarrollar una carretilla autónoma para circular
por una fábrica que un vehículo equivalente por un campo abierto.
Lo que ocurre es que cuando una tecnología
está “madura” como es en la actualidad el uso de la electrónica, entonces ya se
puede adaptar a este entorno más agresivo y con un coste asumible.
LOS
SISTEMAS LiDAR
¿Qué es el LiDAR?: LiDAR
es un principio potente para la detección de objetos y medida de distancias. La palabra LiDAR proviene
de Light Detection And Ranging (detección y medida mediante luz)
¿Cómo funciona?: El
sistema básicamente está compuesto por un láser compuesto por transmisor y
receptor que se usa para medir distancias “a gran escala”. Con ello se consigue
una toma de datos digitales sobre el contorno del terreno, masas arbóreas, etc.
Lo
que hace el sistema es emitir pulsos de luz que se reflejan en el terreno y en
aquellos objetos del terreno. Cuando la parte receptora recibe los reflejos de
los pulsos los transforma en impulsos eléctricos y los interpreta en base al
tiempo que tarda el reflejo del pulso en ser recibido. Si al sistema se le implementa con
información posicional que proporcional un GNSS ya se tiene un modelo digital
del terreno y sus accidentes en 3D.
Una vez que se conoce la tecnología se le pueden
obtener multitud de aplicaciones. Veamos algunas de las más habituales.
Aplicación
agrícola: Se
puede usar LiDAR en la agricultura con diversos fines como es la obtención de
modelos digitales de elevación de masas vegetales (árboles, frutales, viñedos)
y así estimar la superficie foliar y otros parámetros geométricos. Y es que la tecnología LiDAR se indica especialmente
para masas forestales arbóreas por su capacidad, a la postre ventaja, de poder
medir simultáneamente la cota del terreno y la de las copas de los árboles y
así por diferencia obtener la altura de la vegetación y tener visión
tridimensional de la masa vegetal. Ello se consigue con sensores LiDAR capaces de captar múltiples retornos de un mismo pulso emitido. En este tipo de aplicación se suelen usar los sistemas LiDAR con escaneo láser desde un avión que es el que realiza el "barrido" topográfico. El avión cuenta, por supuesto, con sistema GNSS (GPS o similar)
Una derivación sería el uso de técnicas LiDAR
en la agricultura de precisión (AP) levantando “mapas” precisos del
medio con información georreferenciada y sistemas de información geográficos (SIG) sentando las bases de un posible manejo de un mismo campo por zonas (Site-Specific Management)
 |
| Escáner móvil (www.geosistemassrl.com) |
Reconstrucción
arbórea: Es la aplicación en la cual más nos hemos centrado
y a la que dedicaremos el resto del post. La reconstrucción arbórea que nosotros hemos intentado explicar consiste en reconstruir las estructuras de un árbol que, además de sus aplicaciones agrológicas, podría ser útil en la gestión de bosques ya que
disponer de un modelo preciso del arbolado nos indica, por ejemplo, la
susceptibilidad al fuego que puede tener esa masa arbórea.
Topografía: Se ha revolucionado mucho la forma de hacer mapas a gran escala. Una de las técnicas modernas es mediante la generación de modelos digitales del terreno (MDT) que también se pueden obtener mediante la medición de distancias con sistemas basados en LiDAR.
Topografía: Se ha revolucionado mucho la forma de hacer mapas a gran escala. Una de las técnicas modernas es mediante la generación de modelos digitales del terreno (MDT) que también se pueden obtener mediante la medición de distancias con sistemas basados en LiDAR.
 |
| Tractor autónomo CASE IH con sistemas detección y percepción LiDAR, radar y cámaras de vídeo |
 |
| Equipo láser de escaneo |
Otras aplicaciones: En
realidad se le puede sacar mucho provecho en las actualizaciones del catastro
tanto de rústica como urbano. Mediante topografía láser aerotransportada,
vuelos LiDAR, se pueden detectar alturas de las construcciones, naves o casas
de campo pues este tipo de imágenes y de modelos digitales resulta muy sencillo
separar la vegetación, relieve, construcciones…; O bien muy útil en el
planeamiento de rutas para nuevas redes eléctricas
EL
OBJETIVO DEL POST: ESCÁNER LASER TERRESTRE
Uno de los ejemplos de la utilización de este tipo de
tecnologías es el objetivo de este post, en el cual contaremos nuestra
experiencia con el uso de escáners terrestres basados en sensores LiDAR que se montan bien sobre tractor o bien sobre otro tipo
de vehículo de campo. El objetivo es aumentar el conocimiento del medio agrícola. Por ejemplo uno de los proyectos llevados a cabo por el Grupo de
Investigación en AgróTICa y Agricultura de Precisión de la Universitat de Lleida y del Centro Agrotecnio con los que hemos colaborado Valeriano Méndez
(algunos lectores asiduos ya lo conocéis por su aportación a la app para móvil que gratuitamente se puede descargar desde este mismo blog) y yo mismo.
El grupo AgróTICa y Agricultura de Precisión ha
contado para financiar parte de estos trabajos con la aportación del Plan
Estatal de I+D+I del Ministerio de Economía y Competitividad a través del
proyecto AgVANCE (AGL2013-48297-C2-2-R)
¿En
qué consiste?
Imagine el lector que lo que deseamos es tener
una medición precisa de una plantación de frutales, olivos o de vides. Para
ello se necesitará poder reconstruir la geometría de cada árbol. La forma de
hacerlo que se propone aquí es mediante escaneo de los árboles.
El proceso se implementa con un escáner
montado sobre un vehículo terrestre, escáner que incorpora un sensor LiDAR que
lanza un rayo láser. El láser rebota sobre el objeto (suelo, tronco, rama,
hoja, fruto, etc.) y vuelve rebotado. Los fotones de los pulsos reflejados son transformados
en impulsos eléctricos e interpretados por un registrador de datos de alta
velocidad. Lo que se mide es el tiempo que tarda la luz en ir y volver y así
calcular la distancia a la que se encuentra el objeto. Además del sensor LiDAR,
el sistema incluye un receptor GNSS (GPS en combinación con GLONASS) para saber con precisión centimétrica la posición del sensor,
origen de coordenadas del rayo láser. Dado que el rayo se emite en todas las
direcciones de un plano vertical y dado que el tractor va desplazando el
sistema a lo largo de las calles, posteriormente el ordenador que procesará los datos confeccionará un archivo de puntos 3D medidos con coordenadas absolutas (x, y, z)
 |
| Escaneo aéreo LiDAR (Lidar Belize) |
Uno de los problemas es que efectivamente la
marcha del tractor no es uniforme y eso significa que habrá una serie de desviaciones
que ocasionan un arrastre de errores. Para eliminar este tipo de errores se
recurre a colocar unos puntos singulares o “banderolas” de referencia, o por ejemplo incorporando un estabilizador dinámico del sensor para que
siempre esté horizontal o bien incorporando un sensor inercial para medir inclinaciones e incluirlas en el proceso posterior de los datos.
Lo
que se consigue
Tras el escaneo se obtiene una nube de puntos
tridimensional. Esta nube se envía al ordenador y allí con equipos no
necesariamente muy potentes pero si muy constantes (el proceso es costoso en tiempo) se analizan las nubes de puntos.
Es necesario eliminar datos “erróneos”
producidos por “ruidos” electromagnéticos, siempre presentes en el uso de
sensores electrónicos. Lo normal para su eliminación es usar técnicas
estadísticas. También se elimina aquello que no interesa, por ejemplo el suelo.
Con los datos restantes, y siguiendo una
cadena de pasos, ya se puede reconstruir árboles completos (parte leñosa y
foliar) aunque es cierto que hay muchos más estudios en referencia a la
reconstrucción de árboles sin hoja. El método es el mismo, pero efectivamente
al tener hojas el sistema no diferencia bien la estructura entre ramas y hojas.
La experiencia nuestra es sobre árboles sin hoja.
Grafo de Proximidad O PRIMERA FASE
Los pasos a seguir en la reconstrucción de
árboles son:
- Determinación de la conectividad entre puntos próximos
- Obtención de rutas geodésicas desde el pie del árbol a todos los ápices o extremos de las ramas
- Separación de los puntos de acuerdo a su distancia al pie en diferentes niveles
- Reconstrucción de las ramas finales
La primera impresión al visualizar el
escaneado que se ha hecho en campo es que ya se delinean las ramas y queda poco
trabajo por hacer. Pero no es así. Al hacer un zoom se comprueba como se
difumina la nube y aparecen puntos separados sin conexión: ¡La nube no es más
que una lista de 10.000 o 100.000 puntos que no tienen relación entre sí! Lo
que ocurre es que el cerebro con su criterio cognitivo es capaz de darle
sentido.
Formatos de archivo: La mayoría de sistemas LiDAR trabajan con un formato de
archivo binario denominado LAS desarrollado por la American Society for Photogrammetry & Remote Sensing (ASPRS);
Se trata de un formato que permite el intercambio de ficheros que contienen
información de una nube de puntos tridimensional.
 |
| Ejemplo de algoritmo de Dijkstra para 6 vértices |
A
saco con “el saco”: Toca poner orden en el ‘saco’ de puntos. En primer lugar se
establecen las vecindades entre puntos. Se relaciona cada punto con sus vecinos
en función de la proximidad. Una opción para hacerlo es relacionar un punto con
todos los que estén a una distancia “menor
a”. Imagínese que por estar dentro de un mismo circulo, tres puntos A, B y
C son vecinos, cuando en realidad A es vecino de B y B es vecino de C. Ocurre
que B esta entre A y C. Bastaría con establecer la relación A-B y B-C para
tener los 3 puntos perfectamente encadenados. El método se denomina
triangularización de una nube de puntos y lo estableció el matemático ruso
Boris Delaunay. Cuando se dispone de un “saco” tridimensional se llega a una
malla de tetraedros (cuatro aristas que unen cuatro vértices) de la manera más
equilátera posible.
Desgraciadamente el proceso es bastante tedioso
y lento por lo que se emplea una solución de compromiso y que es conectar A con aquellos puntos más próximos en sectores de una esfera con centro A. Las conexiones establecidas entre los distintos puntos definen "el grafo de proximidad"
¿Grafo?: Se denomina así a una serie de puntos que
tiene una estructura que los relaciona. El grafo de proximidad se puede definir
con una matriz o tabla de N filas y N columnas. Si el punto i es vecino del
punto j en la fila i, columna j (posición i,j de la matriz) se pone un 1 en
caso contrario 0. Además en el caso que nos ocupa si i es vecino de j, j es
vecino de i y también pondríamos un 1 en la posición j, i.
Rutas geodésicas O SEGUNDA FASE
Es el momento de establecer otra relación
entre los puntos de la nube. Se llaman caminos de mínima distancia que unen
todos los puntos con el punto inicial o “rutas geodésicas” o incluso “grafo
geodésico”. A cada punto se le relaciona con un predecesor que lleva por el
camino mínimo al punto inicial. El punto inicial elegido es un vértice del pie
del árbol.
La implementación de esta 2ª fase se puede
hacer mediante diferentes algoritmos. Por ejemplo el del especialista en
computación Edsger Djikstra que es un algoritmo fijo que permite unir cada punto con el más cercano.
Si observa el lector el gráfico verá 6 puntos
{a, b, c, d, e, f}, que se conectan entre sí a través de unas aristas (azul)
Por ejemplo el vértice b está conectado con los vértices {a, c, d} Estas
aristas azules serían el grafo de conectividad. Observese también que hay unos
números rojos. Indican la distancia entre vértices (por ejemplo la distancia
entre b y d es 5)
 El grafo geodésico contiene los caminos
mínimos de cada vértice a uno inicial. Seguimos mirando nuestro ejemplo. Si se
decide que el vértice inicial es a, desde el vértice d
hay diferentes caminos que llevan al a: {d, b, a}, {d, c, a} por ejemplo,
siendo el más corto {d, b, a} con 9 unidades.
El grafo geodésico contiene los caminos
mínimos de cada vértice a uno inicial. Seguimos mirando nuestro ejemplo. Si se
decide que el vértice inicial es a, desde el vértice d
hay diferentes caminos que llevan al a: {d, b, a}, {d, c, a} por ejemplo,
siendo el más corto {d, b, a} con 9 unidades.
El algoritmo funciona paso a paso según se
desarrolla en la tabla. Conforme se avanza en la tabla se indica en cada punto
tratado la distancia mínima al punto inicial y su vértice predecesor. Si el
vértice no está tratado indicamos que la distancia es infinita.
- Paso 1: Se inicia el algoritmo con un grafo geodésico vacio y en cada paso se va añadiendo un punto al grafo. Se elige el vértice inicial (a) que tiene distancia geodésica 0 (la distancia de un punto al propio punto es 0) Se calcula la distancia de a hasta los vértices con que esta conectado (b y c) En este paso sólo figura en rojo y como vértice incorporado al grafo geodésico el punto a, los puntos b y c aparecen provisionalmente con una distancia geodésica
- Paso 2: Se elige, de los puntos provisionales (b y c), el que tenga la distancia geodésica menor (en este caso es el c) y se incorpora al grafo geodésico (en rojo en la tabla) Se calcula la distancia geodésica provisional de los puntos conectados a c. Así sucesivamente cada paso consta de dos tareas: primero se elige, de los puntos provisionales (en negro en la tabla), el de distancia menor para pasar al grafo geodésico (el que ponemos en rojo) y segundo se reajusta la distancia de aquellos puntos conectados con el que pasa a rojo.
Al representar en un ordenador los caminos
geodésicos de un árbol escaneado y hacer un zoom suficiente se verá un haz de
hebras que van desde los ápices de las ramas secundarias, hasta el tronco y al
pie pasando por las ramas primarias. Pero una hebra no tiene por qué corresponder
con una rama. Lo normal es que haces de hebras en paralelo se formaran a lo
largo de las distintas ramas del árbol.
La manera de obtener las ramas de las ‘hebras’
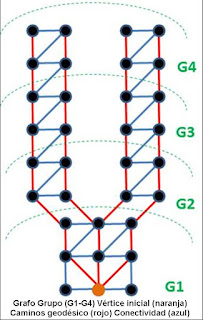
geodésicas es utilizando un paso intermedio, que se denomina grafo de grupos.
Se trocean los caminos en función de su distancia al pie del árbol. Imaginemos
que el camino más largo detectado en la nube es de 4 m y decidimos dividir los
puntos en grupos de 40. Separamos los caminos geodésicos de acuerdo a su
distancia al pie en tramos de 4.000 mm/40 = 100 mm . Así los puntos a 100 mm del pie pertenecen al
grupo 1, los puntos de 100 mm
a 200 mm
al grupo 2, etc. Vamos formando los tramos de ramas con vértices del mismo
grupo. Todos los vértices del grafo geodésico que pertenecen al grupo 1
formarán parte del pie del tronco. Lógicamente en las ramas finales tendremos,
por poner un ejemplo vértices, del grupo 30 que son de distintas ramas en las
que se ha ido desarrollando el árbol. Para separar unos de otros ponemos el
criterio que los vértices estén conectado en el grafo de vecindad. Las hebras
de un mismo grupo conectadas por vecindad serán tramos de una rama. A su vez el
grafo geodésico permite determinar la relación jerárquica entre tramos de rama.
Cuál es la rama predecesora o que ramas descienden de una misma.
 |
| Reconstrucción árbol (www.grap.udl.cat) |
Construcción de ramas finales
Los grupos obtenidos en el proceso anterior se
depuran y se construye la geometría de las ramas. Un proceso común de
depuración es optimizar los centros de gravedad de todos los grupos. Se
comprueba todos los grupos entre si permutando los vértices de forma que el
cambiar un punto de un grupo a otro no aumente las distancias al centro de
gravedad. Es un proceso que busca la mejor compactación posible.
A continuación se suele modelar la rama con un
cilindro, lo que obliga a determinar la dirección del eje. Esto requiere un
método matemático que es similar al que emplea Excel a la hora de calcular la
línea de tendencia de un grupo de puntos (x,y). Se construye una matriz M,
donde en cada fila se pone (x-Gx, y-Gy, z-Gz), siendo G el centro de gravedad
del grupo, la línea de tendencia es el autovector del mayor autovalor de la
matriz Mt.M
Una vuelta de tuerca
 |
| Reconstrucción melocotonero |
El proceso de generación de grupos admite
métodos más sofisticados. Dado que los puntos están en una malla interconectada
puede haber casos en que no esté tan claro en qué grupo debe ir un punto
intermedio. Parece intuitivo que deba ir al grupo que está más cercano. El
método explicado arriba que minimiza la distancia a los centros de gravedad es
sólo uno de los criterios aplicables. Pero no siempre la distancia es un buen
criterio, a veces el criterio que debemos adoptar es con que grupo está mejor
conectado el punto. Por entenderlo supongamos una población que está en el
límite entre dos grandes capitales. ¿A qué capital acudirán frecuentemente los
habitantes, a la más cercana en distancia, o la que tenga más o mejores
carreteras de comunicación?
Ponderar qué punto está mejor interconectado
requiere un alambicado proceso matemático que si acepta el lector se puede
explicar de forma muy resumida diciendo que se trata de construir una matriz de
conectividad (D) análoga a la usada grafo de proximidad, pero que en lugar de 0 y 1 almacena la inversa de la distancia de cada punto i,j (1/d(i,j)) Y otra matriz W diagonal en la cual el valor de cada elemento (i,i) es la suma de
todos los elementos existentes en la columna “i” de la matriz D.
 |
| Reconstrucción perales en espaldera |
Con ambas matrices se construye otra matriz L
= W – D, que se denomina Laplaciana (en honor al matemático Pierre Laplace) Los datos a la “coctelera matemática” y, con mucho tiempo, se calculan los
autovectores y autovalores que ayudará a ponderar la conectividad entre los
puntos de la malla. El truco de la matriz Laplaciana permite obtener una métrica,
una forma de medir los puntos que acerca entre si puntos más interconectados.
Este método es aún más costoso que los anteriores por lo que estamos evaluando si sus beneficios compensan a los elevados incrementos en coste de procesamiento de ordenador.
En el mundo frutícola, disponer de información objetiva y fácil de obtener sobre la estructura y la forma de los árboles es de vital importancia para operaciones como la poda y el aclareo así como para el riego y la fertilización. La generalización de este u otros sistemas y procesos sin duda ayudará a los fruticultores a tomar mejores decisiones en un futuro no muy lejano.
Este método es aún más costoso que los anteriores por lo que estamos evaluando si sus beneficios compensan a los elevados incrementos en coste de procesamiento de ordenador.
En el mundo frutícola, disponer de información objetiva y fácil de obtener sobre la estructura y la forma de los árboles es de vital importancia para operaciones como la poda y el aclareo así como para el riego y la fertilización. La generalización de este u otros sistemas y procesos sin duda ayudará a los fruticultores a tomar mejores decisiones en un futuro no muy lejano.























